1.4 Zustandsdichte

Ein häufig in der Festkörperphysik gebrauchter Begriff ist der Terminus Zustandsdichte, genauer: Zustandsdichte bezüglich der Energie . Zur Definition führen wir in unserem Fall zunächst eine unabhängige Energievariable E ein und bezeichnen die Zahl der Elektronenzustände (Bandzustände), die in dem infinitesimalen Intervall von E bis E + dE liegen, mit g(E) dE. g(E) ist die Zustandsdichte. Für GaAs stellen wir diese in Fig. 1.5 [2] zusammen mit dem im letzten Abschnitt diskutierten E_n(k) - Diagramm in der Weise dar, dass die beiden Energiemaßstäbe übereinstimmen:

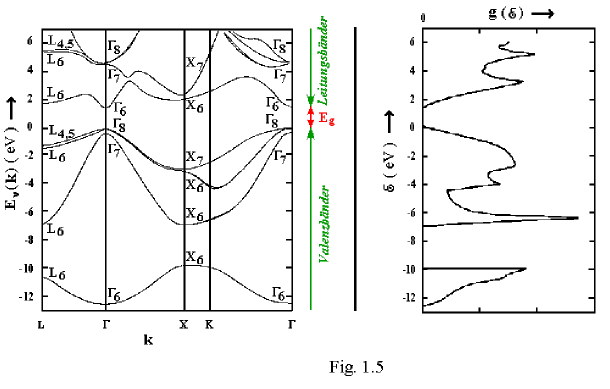
Der Verlauf der Funktion g(E) ist offensichtlich mit dem Verlauf der E_n(k)- Funktionen korreliert. Zwischen beiden Abhängigkeiten besteht der folgende Zusammenhang:

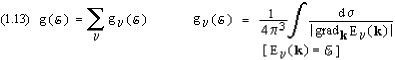
(g(E) und g_n(E) sind hierbei auf die Volumeneinheit bezogen.) Die Integrale werden über Flächen konstanter Energie im k- Raum erstreckt; diese sind für eine gegebene Energie (E) und ein gegebenes Band (n) jeweils durch die Relation

(1.14)     E_n(k) = E

definiert. ds ist das entsprechende Flächenelement. Zu der Summe in Gl. (1.13) tragen alle Bänder bei, die das betrachtete E enthalten, d. h. für die es einen k-Bereich gibt, für den Gl. (1.14) erfüllt ist. In den Bandlücken gibt es natürlich kein derartiges Band; in diesen E - Bereichen verschwindet die Zustandsdichte (zwei Bereiche in Fig. 1.5).

Bei gegebenem E ist g(E) nach Gl. (1.13) umso größer (kleiner), je kleiner (größer) | grad_kE_n (k) | für die in Frage kommenden Bänder ist. Diese Korrelation beruht darauf, dass bei flach (steil) verlaufenden Bändern relativ viele (wenige) Zustände in ein gegebenes Intervall d E fallen (beachte die Äquidistanz der möglichen k-Werte ). Insbesondere entsprechen die scharfen Peaks in g(E) Extrema von E_n (k)- Kurven (Fig. 1.5).